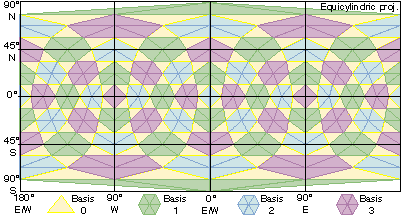
Attractors: Associations of QTM Facets
The numbering we use for QTM facets has some useful properties. First, central facets all end with 0, and corner facets terminate with 1, 2 or 3. Also, the QTM IDs of any two facets sharing an edge differ only in one digit. Finally, each of the 6 corner child facets surrounding a mesh node have the same last digit. If we map the values of the last digit of QTM IDs, we see sets of triangles and hexagons. We call these higher-level elements attractors. The level 3 attractors for the globe are shown in the projected grid below:
By knowing which facets occupy an attractor (several ways have been developed) we are able to associate neighboring facets that are not siblings. This capability, which helps to overcome a limitation of quadtree addressing, is useful in generalizing maps.
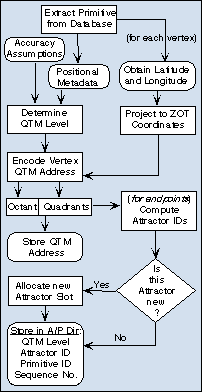
Encoding Vector DataAlthough QTM is like a raster in that it tiles space, we can use it to encode vector data. To do this, we compute a QTM ID for each vertex of each feature, replacing the original geographic coordinates with QTM IDs. To do this, we need either to know or assume how accurate the coordinates are. The stored QTM IDs document variations in spatial accuracy. We can also compute attractor IDs for the line's endpoints, as the diagram to the right shows, for spatial indexing purposes. To generalize the line, we choose an attractor (QTM) level according to the output scale, and generate attractor identifiers for each point on the fly. |
|