Encoding Identifiers for QTM Quadrants
As table 1 indicated, a numeric quadtree identifier (QTM ID) can be computed that specifies any location on a planet within a given linear tolerance, and any such ID can be represented using 64 bits or less of data. The smaller the scale of the source data, the fewer bits are needed to capture it.
For example, the measured location of the building housing the University of Zürich Geography Department on a 1:25K topo map is 47š 23' 48" N, 8š 33' 4" E. Assuming a 50 m measurement error, an 18-digit QTM ID (plus octant) expresses this location as: 1133013130312301002. The location of the author's apartment house, digitized from the same source map, is about 1 km distant at 47° 24' 18" N, 8° 32' 52" E; its QTM ID is 1133013130312011310.
Note that these IDs are constructed by sequencing QTM quadrants in a certain pattern; other orderings would yield different QTM IDs, but translations are always possible.
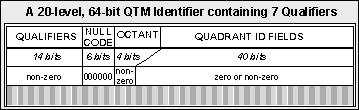
Also note that the first 12 (underlined) QTM ID digits are identical. We thus consult row 12 of table 1 indeed to verify that these locations must be less than 2 km apart. Row 18 then tells us that the 18-digit QTM IDs can be encoded using exactly 40 bits. Variable-length QTM IDs can be constructed by assembling 2-bit quadrant fields in a 64-bit word, preceded by a 4-bit octant field. As the example below shows, most map data does not require full precision (20 levels suffice for 1:25K scale maps). The space remaining in a 64-bit word can be used to store data to qualify a location (coded semantic attributes or metadata), as follows:
Using this low-level encoding, up to 18 bits of qualifying data could have been included; the "null code" needs only 2 (zero) bits to demarcate the qualifiers from the QTM ID.