|
|
|
|
|
|
|
Research Papers
Coastline Data Files
|
  |
The following papers are available for download here in Adobe Portable Document Format (PDF). Please refer to the abstract and notes regarding the individual files.
Encoding and Handling Geospatial Data with Hierarchical Triangular Meshes
NOTES
Author: Geoffrey Dutton
Date: July 1996
Type: Conference paper, Symposium on Spatial Data Handling, Delft, Holland
Reference: Dutton, G. (1996). Encoding and handling geospatial data with hierarchical
triangular meshes. In Kraak, M.J. and Molenaar, M. (eds.) Advances in GIS
Research II. London: Taylor & Francis, 505-518.
ABSTRACT
Planetary geocoding using polyhedral tessellations are a concise and elegant way to organize both local and global geospatial data that respects and documents locational accuracy. After a brief review of several such spatial referencing systems, topological, computational, and geometric properties of one of them are examined. The particular model described in the remainder of the paper -- the octahedral quaternary triangular mesh (O-QTM) -- is being devel-oped to handle and visualize vector-format geodata in a hierarchical triangulated domain. The second section analyzes the geometric regularity of the model, showing that its facets are relatively similar, having vertices spaced uniformly in latitude and longitude, and areas that vary by less than 42 % from their mean sizes. Section 3 describes some fundamental operations on this structure, including mapping from geographic coordinates into O-QTM addresses and back again, filtering map detail through the triangular hierarchy and associating locations that are close together, but in different branches of the tree structure. The final section outlines and illustrates a recent application of O-QTM to map generalization, using its multi-resolution properties to enable multiple cartographic representations to be built from a single hierarchical geospatial database.
Download the PDF version (167 kbytes)
Digital Map Generalization Using a Hierarchical Coordinate System
NOTES
Author: Geoffrey Dutton
Date: April 1997
Type: Conference paper, Symposium on Automated Cartography, Seattle Washington USA
Reference: Dutton, G. (1997). Digital map generalization using a hierarchical coordinate
system, Proc. Auto Carto 13. Seattle WA. Bethesda MD: ACSM-ASPRS, 267-376.
ABSTRACT
The use of hierarchical coordinate systems in geographic information systems (GIS) is a relatively unexplored area, particularly with respect to cartographic generalization techniques. This paper describes a hybrid geospatial data model that enriches vector- topological descriptions of map features by quadtree encoding of vertex locations. It also summarizes methods to encode, analyze, filter and decode vector map data for display at scales smaller than those at which they were captured. Geometric and combinatorial computations are performed either on absolute quadtree addresses, on a world projection or directly on the sphere. The software platform presently only processes one feature class at a time, but is intended to handle more, whether stored as overlaid coverages or as independent or linked objects. 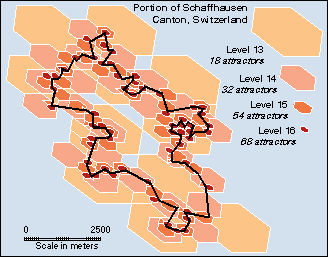Map generalization computations are localized using hierarchical hexagonal and triangular cells called Attractors. This "space-primary" approach to map generalization does not depend upon a hierarchical feature classification scheme, but the two perspectives are related and could be united. This paper describes (1) the quaternary triangular mesh (QTM ) hierarchical location encoding scheme; (2) modeling of cartographic features; (3) some new generalization algorithms and conflict detection techniques; and (4) potential benefits of applying this approach across feature classes.
Download the PDF version (291 kbytes)
Scale, Sinuosity and Point Selection in Digital Line Generalization
NOTES
Author: Geoffrey Dutton
Date: January 1999
Type: Journal article, draft version
Reference: Dutton, G. (1999). Scale, sinuosity and point selection in digital line
generalization. Cartography and Geographic Information Science. 26(1), 33-53.
ABSTRACT
This paper examines some assumptions and results of cartographic line simplification in the digital realm, focusing upon two major aspects of map generalization , scale-specificity and the concept of characteristic points. These are widely regarded as critical controls to generalization, but in our estimation are rarely well-considered or properly applied. First, a look at how scale and shape are treated in various research papers identifies some important conceptual and methodological issues that either have been misconstrued or inadequately treated. We then conduct an empirical analysis with a set of line generalization experiments that control for resolution, detail and sinuosity using four source datasets as examples (two island coastlines digitized at two scales), resulting in about 100 different generalized versions of these figures. These tests systematically explore consequences of linking scale with spatial resolution and a variety of point selection strategies. Graphic results of this exercise are displayed (at scale and enlarged) along with some basic statistics. We feel that most of the common measures of generalization performance rely on dubious assumptions about the value of fidelity of output to source, but at this point we have no specific alternatives to propose in their stead. Rather than proof, then, we offer evidence that whether our methods are used or others are, sensitivity to scale and sinuosity can and must be built in to all digital map generalization toolkits.
Download the main article, PDF version (318 kbytes) NOTE: Some figs are missaligned
Download 6 full-page figures, PDF version (1,510 kbytes)
A Hierarchical Coordinate System for Geoprocessing and Cartography (ch. 1)
NOTES
Author: Geoffrey Dutton
Date: October 1998
Type: Ph.D. Dissertation Chapter 1
Reference: Dutton, G. (1999). A hierarchical coordinate system for geoprocessing and
cartography. Lecture Notes in Earth Science 79. Berlin: Springer-Verlag.
XIX + 231 pp. 97 figs., 12 plates, 16 tabs. ISSN 0930-0317; ISBN 3-540-64980-8
INTRODUCTION
When a mapping agency updates information on topographic maps or navigational charts, usually more than one map is affected by a given change. Often, the largest (most detailed) scale maps are edited first, and the changes then transferred to the appropriate map at the next smaller scale, until either the smallest scale is reached or the edited feature becomes too small to represent. As a result of changes in the world -- or interpretations of it -- marks on maps may change their shape or symbology, relative prominence, locations and labels, according to organizational standards and procedures as well as expert judgement, also known as "cartographic license." This tedious graphic editing process has been described as "working through the scales," as it systematically propagates edits from greater to less detailed cartographic representations. It is one strategy of attacking problems in the art of map generalization, one which specialists from many nations are struggling to understand, formalize and automate. Until about a decade ago, map generalization was practiced almost exclusively by trained cartographers, who learned it by tutelage, example and intuition, deliberately, even rigorously, but not necessarily formally. Manual cartographic generalization involves an unruly set of techniques and precepts that, traditionally, were mainly practiced in public agencies and map publishing houses, and each organization tended to have its own procedures, standards, guidelines and aesthetics for compiling maps in fulfilment of its mission. Only recently has this situation begun to change, but it has done so dramatically and definitively, as maps -- along with every other form of human communication -- have become digital. At the same time, the media, data, tools and enterprises involved in compiling and communicating maps are rapidly becoming global. The author of this thesis, in describing, demonstrating and assessing a specific digital approach to working through scales, hopes to contribute to progress in both map generalization specifically and spatial data handling generally.
Download the PDF version (67 kbytes)
The following four ascii coastline data files are available for download here in Arc/Info ungenerate format. Please refer to the metadata below regarding the contents of each file.
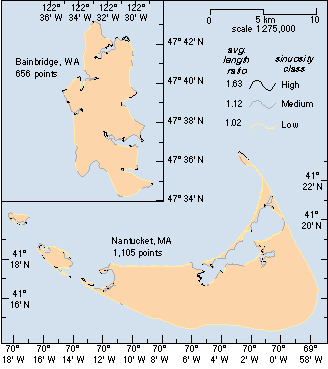
Bainbridge Island, Washington, USA, 1:250K --> download data (9 kbytes)
DATA: 1:250,000 NOAA/NOS digital nautical charts,
vector coordinates in latitude and longitude
SOURCE: Coastline Extractor --
http://crusty.er.usgs.gov/coast/getcoast.html
EXTENT: 122¤ 35' W - 122¤ 25' W (W-E);
47¤ 34' N - 47¤ 43' N (S-N)
WIDTH: 8.62 km; HEIGHT: 16.58 km; AREA: 74.12
km2
LENGTH: 72.13 km; POINTS: 433; AVG SEG LEN: 0.17
km
PROJECTION: None (cordinates are longitude,
latitude, in decimal degrees).
FORMAT: Arc/Info Ungenerate, ascii file, 433
coordinates, 1 polygon
REMARKS: Data originally vectorized by NOS from
digital radar imagery, conditioning unknown. Boundary
segments have been concatenated to form polygons. The 1:250K
scale specified for it implies a resolution between 100 and
200 m (assuming a map resolution of 0.5 mm). As the average
line segment length in the dataset is 200 m, this seems
reasonable.
Bainbridge Island, Washington, USA, 1:80K --> download data (14 kbytes)
DATA: 1:80,000 NOAA/NOS digital nautical charts,
vector coordinates in latitude and longitude
SOURCE: Coastline Extractor --
http://crusty.er.usgs.gov/coast/getcoast.html
EXTENT: 122¤ 35' W - 122¤ 25' W (W-E);
47¤ 34' N - 47¤ 43' N (S-N)
WIDTH: 8.59 km; HEIGHT: 16.41 km; AREA: 70.00
km2
LENGTH: 77.42 km; POINTS: 656; AVG SEG LEN: 0.12
km
PROJECTION: None (cordinates are longitude,
latitude, in decimal degrees).
FORMAT: Arc/Info Ungenerate, ascii file, 656
coordinates, 1 polygon
REMARKS: Data digitized from NOS charts at
1:80,000, possibly with insets digitized from charts as
large as 1:10,000, conditioning unknown. It is possible that
that the area around Nantucket town harbor was digitized
from an inset. The 1:80K scale implies a resolution between
50 and 100 m (assuming a map resolution of 0.5 mm). As the
average line segment length in the dataset is 120 m, this is
not an unreasonable formulation.
Nantucket Island, Masssachusetts, USA, 1:250K --> download data (11 kbytes)
DATA: 1:250,000 NOAA/NOS digital nautical charts,
vector coordinates in latitude and longitude (NOTE: only
main island is included)
SOURCE: Coastline Extractor --
http://crusty.er.usgs.gov/coast/getcoast.html
EXTENT: 70¤ 14' W - 69¤ 58' W (W-E);
41¤ 14' N - 41¤ 23' N (S-N)
WIDTH: 22.00 km; HEIGHT: 17.50 km; AREA: 131.7
km2
LENGTH: 102.5 km; POINTS: 525; AVG SEG LEN: 0.2
km
PROJECTION: None (cordinates are longitude,
latitude, in decimal degrees).
FORMAT: Arc/Info Ungenerate, ascii file, 525
coordinates, 1 polygon
REMARKS: Data originally vectorized by NOS from
digital radar imagery, conditioning unknown. Boundary
segments have been concatenated to form polygons. The 1:250K
scale specified for it implies a resolution between 100 and
200 m (assuming a map resolution of 0.5 mm). As the average
line segment length in the dataset is 200 m, this seems
reasonable.
Nantucket Island, Masssachusetts, USA, 1:80K --> download data (14 kbytes)
DATA: 1:80,000 NOAA/NOS digital nautical charts,
vector coordinates in latitude and longitude (NOTE: only
main island is included)
SOURCE: Coastline Extractor --
http://crusty.er.usgs.gov/coast/getcoast.html
EXTENT: 70¤ 14' W - 69¤ 58' W (W-E);
41¤ 14' N - 41¤ 23' N (S-N)
WIDTH: 22.67 km; HEIGHT: 17.06 km; AREA: 119.9
km2
LENGTH: 125.0 km; POINTS: 867; AVG SEG LEN: 0.14
km
PROJECTION: None (cordinates are longitude,
latitude, in decimal degrees).
FORMAT: Arc/Info Ungenerate, ascii file, 867
coordinates, 1 polygon
REMARKS: Data digitized from NOS charts at
1:80,000, possibly with insets digitized from charts as
large as 1:10,000, conditioning unknown. It is possible that
that the area around Nantucket town harbor was digitized
from an inset. The 1:80K scale implies a resolution between
50 and 100 m (assuming a map resolution of 0.5 mm). As the
average line segment length in the dataset is 140 m, this is
not an unreasonable formulation.